Introduction
In January 1997, the National Institute of Standards and Technology (NIST) initiated a process to replace the Data Encryption Standard (DES) published in 1977. A draft criteria to evaluate potential algorithms was published, and members of the public were invited to provide feedback. The finalized criteria was published in September 1997 which outlined a minimum acceptable requirement for each submission. Four years later in November 2001, Rijndael by Belgian Cryptographers Vincent Rijmen and Joan Daemen that we now refer to as the Advanced Encryption Standard (AES), was announced as the winner.
Since publication, implementations of AES have frequently been optimized for speed. Code that executes the quickest has traditionally taken priority over how much ROM it uses. Developers will use lookup tables to accelerate each step of the encryption process, thus compact implementations are rarely if ever sought after. Our challenge here is to implement AES in the least amount of C and more specifically x86 assembly code. It will obviously result in a slow implementation, and will not be resistant to side-channel analysis, although the latter problem can likely be resolved using conditional move instructions (CMOVcc) if necessary. There are also implementations in 32-bit and 64-bit ARM assembly. The 8-bit version of the C code has been successfully tested on an Arduino Uno.
Parameters
There are three different set of parameters available, with the main difference related to key length. Our implementation will be AES-128, which fits perfectly onto a 32-bit architecture.
| Key Length (Nk words) |
Block Size (Nb words) |
Number of Rounds (Nr) |
|
|---|---|---|---|
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 12 |
| AES-256 | 8 | 4 | 14 |
Structure
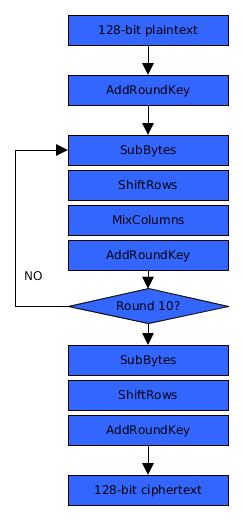
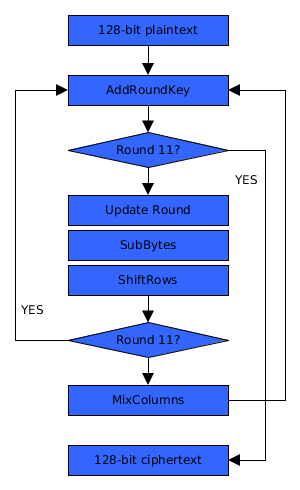
Two IF statements are introduced in order to perform the encryption in one loop. What isn’t included in the illustration below is ExpandRoundKey and AddRoundConstant which generate round keys.
| The first layout here is what we normally see used when describing AES. | The second introduces 2 conditional statements that makes the code more compact. |
|---|---|
|
|
Source in C
The optimizers built into C compilers can sometimes reveal more efficient ways to implement a piece of code. The following performs encryption, and results in approx. 400 bytes of x86 assembly.
#define R(v,n)(((v)>>(n))|((v)<<(32-(n)))) #define F(n)for(i=0;i<n;i++) typedef unsigned char B; typedef unsigned W; // Multiplication over GF(2**8) W M(W x){ W t=x&0x80808080; return((x^t)*2)^((t>>7)*27); } // SubByte B S(B x){ B i,y,c; if(x){ for(c=i=0,y=1;--i;y=(!c&&y==x)?c=1:y,y^=M(y)); x=y;F(4)x^=y=(y<<1)|(y>>7); } return x^99; } void E(B *s){ W i,w,x[8],c=1,*k=(W*)&x[4]; // copy plain text + master key to x F(8)x[i]=((W*)s)[i]; for(;;){ // AddRoundKey, 1st part of ExpandRoundKey w=k[3];F(4)w=(w&-256)|S(w),w=R(w,8),((W*)s)[i]=x[i]^k[i]; // 2nd part of ExpandRoundKey w=R(w,8)^c;F(4)w=k[i]^=w; // if round 11, stop; if(c==108)break; // update round constant c=M(c); // SubBytes and ShiftRows F(16)((B*)x)[(i%4)+(((i/4)-(i%4))%4)*4]=S(s[i]); // if not round 11, MixColumns if(c!=108) F(4)w=x[i],x[i]=R(w,8)^R(w,16)^R(w,24)^M(R(w,8)^w); } }
x86 Overview
Some x86 registers have special purposes, and it’s important to know this when writing compact code.
| Register | Description | Used by |
|---|---|---|
| eax | Accumulator | lods, stos, scas, xlat, mul, div |
| ebx | Base | xlat |
| ecx | Count | loop, rep (conditional suffixes E/Z and NE/NZ) |
| edx | Data | cdq, mul, div |
| esi | Source Index | lods, movs, cmps |
| edi | Destination Index | stos, movs, scas, cmps |
| ebp | Base Pointer | enter, leave |
| esp | Stack Pointer | pushad, popad, push, pop, call, enter, leave |
Those of you familiar with the x86 architecture will know certain instructions have dependencies or affect the state of other registers after execution. For example, LODSB will load a byte from memory pointer in SI to AL before incrementing SI by 1. STOSB will store a byte in AL to memory pointer in DI before incrementing DI by 1. MOVSB will move a byte from memory pointer in SI to memory pointer in DI, before adding 1 to both SI and DI. If the same instruction is preceded by REP (for repeat) then this also affects the CX register, decreasing by 1.
Initialization
The s parameter points to a 32-byte buffer containing a 16-byte plain text and 16-byte master key which is copied to the local buffer x.
A copy of the data is required, because both will be modified during the encryption process. ESI will point to s while EDI will point to x. EAX will hold Rcon value declared as c. ECX will be used exclusively for loops, and EDX is a spare register for loops which require an index starting position of zero. There’s a reason to prefer EAX than other registers. Byte comparisons are only 2 bytes for AL, while 3 for others.
// 2 vs 3 bytes /* 0001 */ "\x3c\x6c" /* cmp al, 0x6c */ /* 0003 */ "\x80\xfb\x6c" /* cmp bl, 0x6c */ /* 0006 */ "\x80\xf9\x6c" /* cmp cl, 0x6c */ /* 0009 */ "\x80\xfa\x6c" /* cmp dl, 0x6c */
In addition to this, one operation requires saving EAX in another register, which only requires 1 byte with XCHG. Other registers would require 2 bytes
// 1 vs 2 bytes /* 0001 */ "\x92" /* xchg edx, eax */ /* 0002 */ "\x87\xd3" /* xchg ebx, edx */
Setting EAX to 1, our loop counter ECX to 4, and EDX to 0 can be accomplished in a variety of ways requiring only 7 bytes. The alternative for setting EAX here would be : XOR EAX, EAX; INC EAX
// 7 bytes /* 0001 */ "\x6a\x01" /* push 0x1 */ /* 0003 */ "\x58" /* pop eax */ /* 0004 */ "\x6a\x04" /* push 0x4 */ /* 0006 */ "\x59" /* pop ecx */ /* 0007 */ "\x99" /* cdq */
Another way …
// 7 bytes /* 0001 */ "\x31\xc9" /* xor ecx, ecx */ /* 0003 */ "\xf7\xe1" /* mul ecx */ /* 0005 */ "\x40" /* inc eax */ /* 0006 */ "\xb1\x04" /* mov cl, 0x4 */
And another..
// 7 bytes /* 0000 */ "\x6a\x01" /* push 0x1 */ /* 0002 */ "\x58" /* pop eax */ /* 0003 */ "\x99" /* cdq */ /* 0004 */ "\x6b\xc8\x04" /* imul ecx, eax, 0x4 */
ESI will point to s which contains our plain text and master key. ESI is normally reserved for read operations. We can load a byte with LODS into AL/EAX, and move values from ESI to EDI using MOVS. Typically we see stack allocation using ADD or SUB, and sometimes (very rarely) using ENTER. This implementation only requires 32-bytes of stack space, and PUSHAD which saves 8 general purpose registers on the stack is exactly 32-bytes of memory, executed in 1 byte opcode. To illustrate why it makes more sense to use PUSHAD/POPAD instead of ADD/SUB or ENTER/LEAVE, the following are x86 opcodes generated by assembler.
// 5 bytes /* 0000 */ "\xc8\x20\x00\x00" /* enter 0x20, 0x0 */ /* 0004 */ "\xc9" /* leave */ // 6 bytes /* 0000 */ "\x83\xec\x20" /* sub esp, 0x20 */ /* 0003 */ "\x83\xc4\x20" /* add esp, 0x20 */ // 2 bytes /* 0000 */ "\x60" /* pushad */ /* 0001 */ "\x61" /* popad */
Obviously the 2-byte example is better here, but once you require more than 96-bytes, usually ADD/SUB in combination with a register is the better option.
; ***************************** ; void E(void *s); ; ***************************** _E: pushad xor ecx, ecx ; ecx = 0 mul ecx ; eax = 0, edx = 0 inc eax ; c = 1 mov cl, 4 pushad ; alloca(32) ; F(8)x[i]=((W*)s)[i]; mov esi, [esp+64+4] ; esi = s mov edi, esp pushad add ecx, ecx ; copy state + master key to stack rep movsd popad
Multiplication
A pointer to this function is stored in EBP, and there are three reasons to use EBP over other registers:
- EBP has no 8-bit registers, so we can’t use it for any 8-bit operations.
- Indirect memory access requires 1 byte more for index zero.
- The only instructions that use EBP are ENTER and LEAVE.
// 2 vs 3 bytes for indirect access /* 0001 */ "\x8b\x5d\x00" /* mov ebx, [ebp] */ /* 0004 */ "\x8b\x1e" /* mov ebx, [esi] */
When writing compact code, EBP is useful only as a temporary register or pointer to some function.
; ***************************** ; Multiplication over GF(2**8) ; ***************************** call $+21 ; save address push ecx ; save ecx mov cl, 4 ; 4 bytes add al, al ; al <<= 1 jnc $+4 ; xor al, 27 ; ror eax, 8 ; rotate for next byte loop $-9 ; pop ecx ; restore ecx ret pop ebp
SubByte
In the SubBytes step, each byte in the state matrix is replaced with
using an 8-bit substitution box. The S-box is derived from the multiplicative inverse over
, and we can implement SubByte purely using code.
; ***************************** ; B SubByte(B x) ; ***************************** sub_byte: pushad test al, al ; if(x){ jz sb_l6 xchg eax, edx mov cl, -1 ; i=255 ; for(c=i=0,y=1;--i;y=(!c&&y==x)?c=1:y,y^=M(y)); sb_l0: mov al, 1 ; y=1 sb_l1: test ah, ah ; !c jnz sb_l2 cmp al, dl ; y!=x setz ah jz sb_l0 sb_l2: mov dh, al ; y^=M(y) call ebp ; xor al, dh loop sb_l1 ; --i ; F(4)x^=y=(y<<1)|(y>>7); mov dl, al ; dl=y mov cl, 4 ; i=4 sb_l5: rol dl, 1 ; y=R(y,1) xor al, dl ; x^=y loop sb_l5 ; i-- sb_l6: xor al, 99 ; return x^99 mov [esp+28], al popad ret
AddRoundKey
The state matrix is combined with a subkey using the bitwise XOR operation.
; ***************************** ; AddRoundKey ; ***************************** ; F(4)s[i]=x[i]^k[i]; pushad xchg esi, edi ; swap x and s xor_key: lodsd ; eax = x[i] xor eax, [edi+16] ; eax ^= k[i] stosd ; s[i] = eax loop xor_key popad
AddRoundConstant
There are various cryptographic attacks possible against AES without this small, but important step. It protects against the Slide Attack, first described in 1999 by David Wagner and Alex Biryukov. Without different round constants to generate round keys, all the round keys will be the same.
; ***************************** ; AddRoundConstant ; ***************************** ; *k^=c; c=M(c); xor [esi+16], al call ebp
ExpandRoundKey
The operation to expand the master key into subkeys for each round of encryption isn’t normally in-lined. To boost performance, these round keys are precomputed before the encryption process since you would only waste CPU cycles repeating the same computation which is unnecessary. Compacting the AES code into a single call requires in-lining the key expansion operation. The C code here is not directly translated into x86 assembly, but the assembly does produce the same result.
; *************************** ; ExpandRoundKey ; *************************** ; F(4)w<<=8,w|=S(((B*)k)[15-i]);w=R(w,8);F(4)w=k[i]^=w; pushad add esi,16 mov eax, [esi+3*4] ; w=k[3] ror eax, 8 ; w=R(w,8) exp_l1: call S ; w=S(w) ror eax, 8 ; w=R(w,8); loop exp_l1 mov cl, 4 exp_l2: xor [esi], eax ; k[i]^=w lodsd ; w=k[i] loop exp_l2 popad
Combining the steps
An earlier version of the code used separate AddRoundKey, AddRoundConstant and ExpandRoundKey, but since these steps all relate to using and updating the round key, the three steps are combined in order to reduce the number of loops, thus shaving off a few bytes.
; ***************************** ; AddRoundKey, AddRoundConstant, ExpandRoundKey ; ***************************** ; w=k[3];F(4)w=(w&-256)|S(w),w=R(w,8),((W*)s)[i]=x[i]^k[i]; ; w=R(w,8)^c;F(4)w=k[i]^=w; pushad xchg eax, edx xchg esi, edi mov eax, [esi+16+12] ; w=R(k[3],8); ror eax, 8 xor_key: mov ebx, [esi+16] ; t=k[i]; xor [esi], ebx ; x[i]^=t; movsd ; s[i]=x[i]; ; w=(w&-256)|S(w) call S ; al=S(al); ror eax, 8 ; w=R(w,8); loop xor_key ; w=R(w,8)^c; xor eax, edx ; w^=c; ; F(4)w=k[i]^=w; mov cl, 4 exp_key: xor [esi], eax ; k[i]^=w; lodsd ; w=k[i]; loop exp_key popad
ShiftRows
ShiftRows cyclically shifts the bytes in each row of the state matrix by a certain offset. The first row is left unchanged. Each byte of the second row is shifted one to the left, with the third and fourth rows shifted by two and three respectively. Because it doesn’t matter about the order of SubBytes and ShiftRows, they’re combined in one loop.
; *************************** ; ShiftRows and SubBytes ; *************************** ; F(16)((B*)x)[(i%4)+(((i/4)-(i%4))%4)*4]=S(((B*)s)[i]); pushad mov cl, 16 shift_rows: lodsb ; al = S(s[i]) call sub_byte push edx mov ebx, edx ; ebx = i%4 and ebx, 3 ; shr edx, 2 ; (i/4 - ebx) % 4 sub edx, ebx ; and edx, 3 ; lea ebx, [ebx+edx*4] ; ebx = (ebx+edx*4) mov [edi+ebx], al ; x[ebx] = al pop edx inc edx loop shift_rows popad
MixColumns
The MixColumns transformation along with ShiftRows are the main source of diffusion. Each column is treated as a four-term polynomial , where the coefficients are elements over
, and is then multiplied modulo
with a fixed polynomial
; ***************************** ; MixColumns ; ***************************** ; F(4)w=x[i],x[i]=R(w,8)^R(w,16)^R(w,24)^M(R(w,8)^w); pushad mix_cols: mov eax, [edi] ; w0 = x[i]; mov ebx, eax ; w1 = w0; ror eax, 8 ; w0 = R(w0,8); mov edx, eax ; w2 = w0; xor eax, ebx ; w0^= w1; call ebp ; w0 = M(w0); xor eax, edx ; w0^= w2; ror ebx, 16 ; w1 = R(w1,16); xor eax, ebx ; w0^= w1; ror ebx, 8 ; w1 = R(w1,8); xor eax, ebx ; w0^= w1; stosd ; x[i] = w0; loop mix_cols popad jmp enc_main
Counter Mode (CTR)
Block ciphers should never be used in Electronic Code Book (ECB) mode, and the ECB Penguin illustrates why.

As you can see, blocks of the same data using the same key result in the exact same ciphertexts; this is why modes of encryption were invented. Galois/Counter Mode (GCM) is authenticated encryption that uses Counter (CTR) mode to provide confidentiality. The concept of CTR mode which turns a block cipher into a stream cipher was first proposed by Whitfield Diffie and Martin Hellman in their 1979 publication, Privacy and Authentication: An Introduction to Cryptography. CTR mode works by encrypting a nonce and counter, then using the ciphertext to encrypt our plain text using a simple XOR operation. Since AES encrypts 16-byte blocks, a counter can be 8-bytes, and a nonce 8-bytes.
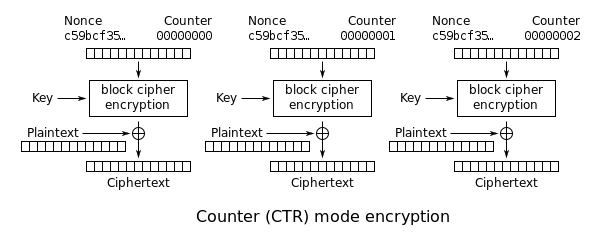
The following is a very simple implementation of this mode using the AES-128 implementation.
// encrypt using Counter (CTR) mode void encrypt(W l, B*c, B*p, B*k){ W i,r; B t[32]; // copy master key to local buffer F(16)t[i+16]=k[i]; while(l){ // copy counter+nonce to local buffer F(16)t[i]=c[i]; // encrypt t E(t); // XOR plaintext with ciphertext r=l>16?16:l; F(r)p[i]^=t[i]; // update length + position l-=r;p+=r; // update counter for(i=16;i>0;i--) if(++c[i-1])break; } }
In assembly.
; void encrypt(W len, B *ctr, B *in, B *key) _encrypt: pushad lea esi,[esp+32+4] lodsd xchg eax, ecx ; ecx = len lodsd xchg eax, ebp ; ebp = ctr lodsd xchg eax, edx ; edx = in lodsd xchg esi, eax ; esi = key pushad ; alloca(32) ; copy master key to local buffer ; F(16)t[i+16]=key[i]; lea edi, [esp+16] ; edi = &t[16] movsd movsd movsd movsd aes_l0: xor eax, eax jecxz aes_l3 ; while(len){ ; copy counter+nonce to local buffer ; F(16)t[i]=ctr[i]; mov edi, esp ; edi = t mov esi, ebp ; esi = ctr push edi movsd movsd movsd movsd ; encrypt t call _E ; E(t) pop edi aes_l1: ; xor plaintext with ciphertext ; r=len>16?16:len; ; F(r)in[i]^=t[i]; mov bl, [edi+eax] ; xor [edx], bl ; *in++^=t[i]; inc edx ; inc eax ; i++ cmp al, 16 ; loopne aes_l1 ; while(i!=16 && --ecx!=0) ; update counter xchg eax, ecx ; mov cl, 16 aes_l2: inc byte[ebp+ecx-1] ; loopz aes_l2 ; while(++c[i]==0 && --ecx!=0) xchg eax, ecx jmp aes_l0 aes_l3: popad popad ret
Full source code
The following is for AES-128, AES-256 on 8-bit or 32-bit and 64-bit architectures. Using a table lookup for the sbox is enabled by default because the DYNAMIC method is incredibly slow.
// Multiplication over GF(2**8) #if AES_INT_LEN == 1 #define M(x)(((x)<<1)^((-((x)>>7))&0x1b)) #else u32 M(u32 x) { u32 t=x&0x80808080; return((x^t)<<1)^((t>>7)*0x1b); } #endif // the sbox array is used by default for optimal speed #ifndef DYNAMIC u8 sbox[256]= {0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79, 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 }; #define S(x) sbox[x] #else // SubByte u8 S(u8 x) { u8 i,y,c; if(x) { for(c=i=0,y=1;--i;y=(!c&&y==x)?c=1:y,y^=M(y)); x=y; for(i=0;i<4;i++) { x^=y=(y<<1)|(y>>7); } } return x^99; } #endif #if AES_INT_LEN == 1 // 128-bit version for 8-bit architectures void aes_ecb(void *mk, void *data) { u8 a,b,c,d,i,j,t,x[AES_BLK_LEN], k[AES_KEY_LEN],rc=1,*s=(u8*)data; // copy 128-bit plain text + 128-bit master key to x for(i=0;i<AES_BLK_LEN;i++) { x[i]=s[i], k[i]=((u8*)mk)[i]; } for(;;) { // AddRoundKey for(i=0;i<AES_BLK_LEN;i++) { s[i]=x[i]^k[i]; } // if round 11, stop if(rc==108)break; // AddConstant k[0]^=rc; rc=M(rc); // ExpandKey for(i=0;i<4;i++) { k[i]^=S(k[12+((i-3)&3)]); } for(i=0;i<12;i++) { k[i+4]^=k[i]; } // SubBytes and ShiftRows for(i=0;i<AES_BLK_LEN;i++) { x[(i&3)+((((u32)(i>>2)-(i&3))&3)<<2)]=S(s[i]); } // if not round 11 if(rc!=108) { // MixColumns for(i=0;i<AES_BLK_LEN;i+=4) { a=x[i],b=x[i+1],c=x[i+2],d=x[i+3]; for(j=0;j<4;j++) { x[i+j]^=a^b^c^d^M(a^b); t=a,a=b,b=c,c=d,d=t; } } } } } #else // 32-bit or 64-bit versions #if AES_KEY_LEN == 32 void aes_ecb(void *mk, void *data) { u32 c=1,i,r=0,w,x[4],k[8], *s=(u32*)data; // copy 128-bit plain text for(i=0;i<4;i++) { x[i] = s[i]; } // copy 256-bit master key for(i=0;i<8;i++) { k[i] = ((u32*)mk)[i]; } for(;;) { // 1st part of ExpandKey w=k[r?3:7]; for(i=0;i<4;i++) { w=(w&-256) | S(w&255),w=R(w,8); } // AddConstant, update constant if(!r)w=R(w,8)^c,c=M(c); // AddRoundKey, 2nd part of ExpandKey for(i=0;i<4;i++) { ((u32*)s)[i]=x[i]^k[r*4+i], w=k[r*4+i]^=w; } // if round 15, stop if(c==27) break; r=(r+1)&1; // SubBytes and ShiftRows for(i=0;i<AES_BLK_LEN;i++) { ((u8*)x)[(i%4)+(((i/4)-(i%4))%4)*4]=S(((u8*)s)[i]); } // if not round 15, MixColumns if((c!=128) | r) { for(i=0;i<4;i++) { w=x[i],x[i]=R(w,8)^R(w,16)^R(w,24)^M(R(w,8)^w); } } } } #else void aes_ecb(void *mk, void *data) { u32 c=1,i,w,x[4],k[4],*s=(u32*)data; // copy 128-bit plain text + 128-bit master key to x for(i=0;i<4;i++) { x[i]=s[i], k[i]=((u32*)mk)[i]; } for(;;) { // 1st part of ExpandKey w=k[3]; for(i=0;i<4;i++) { w=(w&-256)|S(w&255), w=R(w,8); } // AddConstant, AddRoundKey, 2nd part of ExpandKey w=R(w, 8)^c; for(i=0;i<4;i++) { ((u32*)s)[i]=x[i]^k[i], w=k[i]^=w; } // if round 11, stop if(c==108)break; // update constant c=M(c); // SubBytes and ShiftRows for(i=0;i<AES_BLK_LEN;i++) { ((u8*)x)[(i%4)+(((i/4)-(i%4))%4)*4]=S(((u8*)s)[i]); } // if not round 11, MixColumns if(c!=108) { for(i=0;i<4;i++) { w=x[i],x[i]=R(w,8)^R(w,16)^R(w,24)^M(R(w,8)^w); } } } } #endif #endif #ifdef CTR // encrypt using Counter (CTR) mode void aes_ctr(u32 len, void *ctr, void *data, void *mk) { u8 i, r, t[AES_BLK_LEN], *p=data, *c=ctr; while(len) { // copy counter+nonce to local buffer for(i=0;i<AES_BLK_LEN;i++)t[i] = c[i]; // encrypt t aes_ecb(mk, t); // XOR plaintext with ciphertext r = len > AES_BLK_LEN ? AES_BLK_LEN : len; for(i=0;i<r;i++) p[i] ^= t[i]; // update length + position len -= r; p += r; // update counter. for(i=AES_BLK_LEN;i!=0;i--) if(++c[i-1]) break; } } #endif
Summary
The final assembly code for ECB mode is 205 bytes, and 272 for CTR mode. You can find sources here.